はじめに
近年、大規模言語モデル(LLM)をはじめとするニューラルネットワークの能力は急速に向上していますが、その内部で実際にどのようなアルゴリズムが実行されているのかについては、ほとんど理解されていません。
メカニズム的解釈性(Mechanistic Interpretability)とは、ニューラルネットワークをリバースエンジニアリングし、その内部の計算過程を完全に理解することを目指す分野です。しかし、トランスフォーマーモデルの解釈を困難にしている大きな要因の一つに、重みや活性化が直接的に人間にとって理解可能な概念に対応していないことがあります。特に、密なモデル(Dense models)では、一つのニューロンが複数の概念を表現する「重ね合わせ(Superposition)」という現象が発生していることが原因の一つとして仮説立てられています。
本稿で紹介する研究では、OpenAIがこの課題に対処するため、重みの大半をゼロに制約した「重みスパースなトランスフォーマー(Weight-sparse transformers)」を訓練するという新しいパラダイムを導入しました。これにより、各ニューロンの接続を数本に限定し、計算回路を大幅に単純化することで、人間が完全に理解できるレベルの回路抽出に成功しています。
解説論文
- 論文タイトル:Weight-sparse transformers have interpretable circuits
- 論文URL:https://cdn.openai.com/pdf/41df8f28-d4ef-43e9-aed2-823f9393e470/circuit-sparsity-paper.pdf
- 発表者:Leo Gao, Achyuta Rajaram, Jacob Coxon, Soham V. Govande, Bowen Baker, Dan Mossing ら (OpenAI)
・あくまで個人の理解に基づくものであり、正確性に問題がある場合がございます。
必ず参照元論文をご確認ください。
・本記事内での画像は、上記論文より引用しております。
要点
- 解釈性の向上と回路の単純化: 重みをスパース化(非ゼロの重みを制限)することで、モデルの計算が大幅に単純化され、タスク固有の回路(計算経路)が、同等の事前学習損失を持つ密なモデルと比較して約16分の1のサイズで抽出可能となった。
- 人間による理解の検証: 抽出された回路には、「シングルクォートに続くトークン」や「リストのネストの深さ」など、自然な概念に対応するニューロンやチャネルが含まれており、それらの接続は直感的に解釈可能である。
- 回路の必要十分性の検証: 抽出されたコンパクトな回路が、モデルの挙動にとって必要かつ十分であることを、平均アブレーション(Mean-ablation)という検証手法を用いて厳密に示した。
- スケールによる改善: モデルサイズを拡大すると、能力(Capability)と解釈性(Interpretability)のトレードオフの関係を示すフロンティアが改善することがわかった。
- 既存密モデルへの応用: 「ブリッジ(Bridges)」という手法を用いることで、重みスパースなモデルの知見を、既存の訓練済み密モデルの解釈にも応用できる可能性を示唆した。
詳細解説
項目にそって解説していきます。
1. Introduction (導入)
大規模言語モデル(LLM)などのニューラルネットワークは近年、その能力を急速に向上させていますが、それらが内部でどのようなアルゴリズムを実装しているのかについて、我々はほとんど理解していません。
我々が目指す「メカニズム的解釈性(Mechanistic Interpretability)」は、ニューラルネットワークをリバースエンジニアリングし、その内部の計算アルゴリズムを完全に理解することを目指しています。
トランスフォーマーの解釈を困難にしている主要な課題は、活性化(activations)や重み(weights)が、人間が直感的に理解できる概念に直接対応していないことです。例えば、ニューロンは人間にとって予測不可能なパターンで活性化します。
この現象の原因として「重ね合わせ(Superposition)」が仮説として立てられています。これは、密なモデル(Dense models)が、実際にはより大規模で「絡まりのない(untangled)」疎なネットワークの計算を近似しているという考え方です。
既存のアプローチでは、活性化が疎になるような基底を学習し、その基底内でのモデルの計算を理解しようとしていますが、これらの手法は、部分的にしか理解されていない複雑な計算を抽象化して回路を導出するため、結果として得られた回路が、モデルの真のメカニズムだけでなく、選択された抽象化を反映している可能性があるという制約があります。
本研究では、この課題に対し、重みの大半をゼロに制約する(重みの \(L_0\) ノルム、すなわち非ゼロの重みの数を小さくする)という新しいパラダイムを導入しました。
この制約は、モデルの計算を劇的に単純化します。各ニューロンは少数の残差チャネルから読み書きすることしかできないため、モデルは、概念の表現を複数の残差チャネルに分散させたり、単一の概念を表現するために必要以上のニューロンを使用したりすることを控えるようになります。
結果として、我々は、最低レベルの抽象化においても完全に理解できる、実質的により単純で一般的な回路を得ることに成功しました。

我々は、この重みスパースなモデルが、異なるタスクに対して「絡まりのない(disentangled)回路」を学習することを、タスクを実行するために必要な最小の回路を分離し、それがコンパクトであることを示すことで証明しました。
抽出された回路内では、ニューロンの活性化が「シングルクォートに続くトークン」や「リストのネストの深さ」といった単純な概念に対応し、重みがこれらの概念間の直感的な接続を符号化していることが判明しました。
さらに、これらの回路がモデルの挙動にとって必要かつ十分であることを、厳密に検証しています。具体的には、回路に含まれないノードを平均アブレーション(Mean-ablating、活性化を事前学習分布における平均値に固定すること)してもタスク損失は維持され、逆に回路内のノードを削除するとタスク損失が大きく損なわれることが示されました。
重みスパースな訓練は解釈性にとって大きな利点があるものの、計算効率が悪く、フロンティアモデル(最先端の高性能モデル)の能力に到達することは難しいという重大な制約があります。これは、現代のGPUが疎行列演算に不向きな構造を採用していることに起因します。
しかし、我々は、各層に「ブリッジ(Bridges)」を用いて、重みスパースモデルの表現をターゲットとなる密なモデルの表現に結合させることで、訓練済みの密モデルの挙動を理解するためにこの手法を応用できる予備的な結果を示しました。
2. Methods (手法)
ここでは、重みスパースなモデルを訓練し、その回路を抽出するための具体的な手法について説明します。
具体的には、重みの大半がゼロであるトランスフォーマーモデルを事前学習した後、モデルがシンプルなタスクを実行するために使う最小限の計算経路(回路)を、新しいプルーニング(枝刈り)手法で分離します。この回路は、ニューロンや残差チャネルの読み書きといった最小単位の「ノード」と、非ゼロの重みである「エッジ」で定義され、回路内のエッジ数が少ないほど解釈性が高いと評価されます。
2.1. Sparse Training (スパースな学習)
アーキテクチャ:モデルのアーキテクチャは、GPT-2に類似したデコーダーオンリーのトランスフォーマーを使用しています。すべての重みとバイアスにスパース性を適用しており、最もスパースなモデルでは、約1000個に1個の重みしか非ゼロではありません。重みのスパース性は、重みの非ゼロの数を示す \(L_0\) ノルムが小さいという制約によって定義されます。また、ニューラルネットワークの層の出力に適用される標準的な正規化手法であるLayerNormの代わりに、RMSNorm(Root Mean Square Layer Normalization)を使用しています。これにより、ゼロの値が残差ストリーム(Residual Stream)内で特権的な意味を持つことを確実にします。
※LayerNormは、入力ベクトルに対して「平均を引く」操作を行います。これは、入力の統計量を正規化する上で有効ですが、たとえ入力となる残差ストリームの活性化がほとんどゼロ(つまり情報が疎)であったとしても、平均を引くことで、強制的にその値が非ゼロにシフトされてしまう可能性があります。これにより、「情報がない状態」を示すはずの「ゼロ」が曖昧になってしまいます。RMSNormは、二乗平均平方根(RMS: Root Mean Square、値の二乗の平均の平方根)で割って正規化を行うことで、平均を引く操作がないため、活性化がゼロに近い値を持つ場合、RMSNormを通過した後もゼロに近い状態が維持されやすくなります。
活性化のスパース性:重みのスパース性だけでなく、活性化(Activation)のスパース性も強制されています。具体的には、モデル内のさまざまな場所で、値の大きい上位 \(k\) 個(通常は次元の1/4)のみを残し、それ以外をゼロにする AbsTopK 活性化関数を適用しています。
最適化:最適化にはAdamWオプティマイザを使用します。\(L_0\) 重みスパース性の制約を強制するため、各訓練ステップでAdamWを適用した後、各重み行列のマグニチュード(絶対値)が最大のものだけを残し、それ以外をゼロにします。訓練の過程で、モデルが完全に密な状態から目標とする \(L_0\) に向かって線形にスパース性を徐々に高めていく(アニーリングする)手法を採用しています。
2.2. Measuring interpretability (解釈性の測定)
解釈性の測定方法:解釈性を評価するために、本研究では、モデルが特定のタスクを実行するために使用する小さなスパース回路を、新しいプルーニング(枝刈り)手法を用いて分離します。解釈可能なモデルとは「絡まりにくい(untangle)」はずであるという考えに基づき、個々の挙動はコンパクトで独立した回路によって実装されていると仮定されます。
ノードとエッジの定義:回路は、エッジで接続されたノードの集合として定義されます。
- ノード(Node):個々のニューロン、アテンションチャネル、残差チャネルの読み取り、または残差チャネルの書き込みといった、最大限に細粒度の構成要素を指します。
- エッジ(Edge):重み行列における非ゼロのエントリであり、2つのノードを接続します。
主要な定量的解釈性指標として、手作業で作成されたタスク全体における、回路内のエッジ数の幾何平均が報告されています。
プルーニング:各タスクに対し、特定の目標損失(Target Loss)を達成できる最小の回路を見つけ出すためにモデルをプルーニングします。プルーニングの際、削除されたノードは「平均アブレーション(Mean-ablated)」されます。これは、それらの活性化が、事前学習分布における平均活性化値に固定されることを意味します。本研究では、タスク損失と回路サイズの双方を最小化する目的関数を用いて、マスクパラメータを訓練する構造化プルーニングアルゴリズムを導入しています。
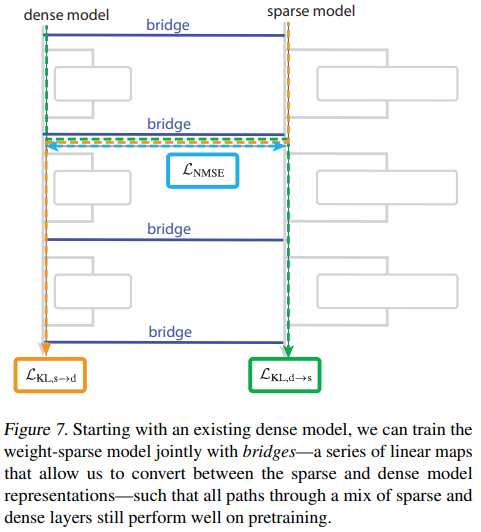
2.3. Bridges (ブリッジ)
訓練済みの密なモデルの挙動を理解するために、重みスパースなモデルを密なモデルと並行して訓練する手法を提案しています。
ブリッジの構成:ブリッジは、密なモデルとスパースなモデルの活性化を層ごとにマッピングするエンコーダーとデコーダーで構成されます。エンコーダーは密な活性化をスパースな活性化に、デコーダーはスパースな活性化を密な活性化に変換します。
損失項:ブリッジは、スパースモデルの計算が密モデルの計算と一致するように訓練されます。この訓練では、通常の事前学習損失に加えて、以下の3つのブリッジ損失項が使用されます。
- 正規化MSE項(\(L_{NMSE}\)): ブリッジが密な活性化からスパースな活性化を、またはその逆を正確に予測するように訓練する。
- KL項 (\(L_{KL, d \to s}\) と \(L_{KL, s \to d}\)): 密な層とスパースな層が混在したハイブリッドな順伝播を実行し、その出力が元の密モデルの出力と低いKLダイバージェンスを持つように、スパースモデルの重みを訓練する。
3. Results (結果)
3.1. Weight sparsity improves interpretability (重みのスパース性が解釈性を向上させる)
本研究では、重みのスパース性がモデルがより小さな回路を学習することを可能にすることを示しました。
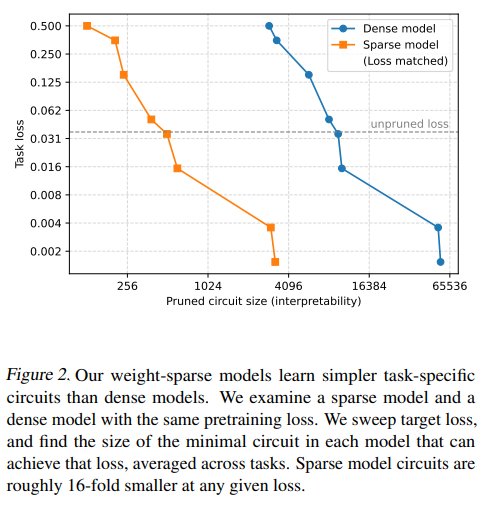
- 回路サイズの比較: 事前学習損失が同程度の密なモデルとスパースなモデルを比較した結果、重みスパースなモデルをプルーニングすることで得られる回路は、タスクにおいて密なモデルの回路よりも平均して約16倍小さいことが判明しました。このことは、重みスパースなモデルにおいて、単純な挙動のための回路が密なモデルよりもはるかに「分離しており(disentangled)」、「局所化可能である(localizable)」ことを示しています。
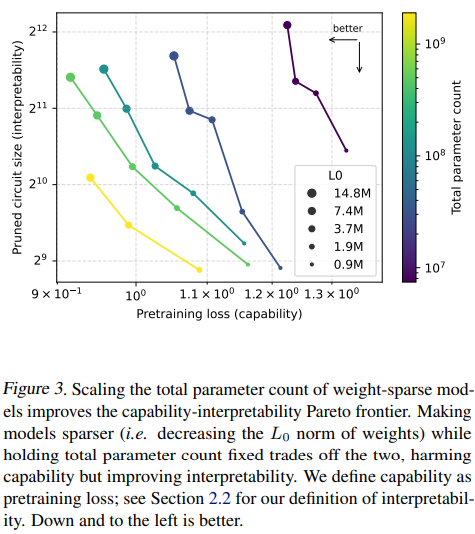
- 能力と解釈性のフロンティア: モデルサイズをスケールアップさせると、能力(事前学習損失)と解釈性(プルーニングされた回路サイズ)のパレートフロンティアが改善します。重み \(L_0\) を固定し、より大きなモデルを使用すると、能力と解釈性の両方が向上することが確認されました。
3.2. Qualitative circuit investigations (定性的な回路の調査)
回路サイズは解釈性の代理指標に過ぎないため、抽出された回路が人間にとって理解可能なアルゴリズムを実装しているかを検証するため、いくつかのタスクについて手動で回路を分析しました。
3.2.1. CLOSING STRINGS (文字列を閉じる)
入力された文字列がシングルクォート(’)またはダブルクォート(”)のどちらで開かれているかに応じて、対応するクォートで文字列を閉じるタスク(single double quote)の回路が分析されました。
これは、1つのMLP層にある2つのニューロンと、1つのアテンションヘッドを用いた2ステップのプロセスで実行されます。
- エンコーディング: 最初のMLP層(0.mlp)が、トークン埋め込み((“と(‘)を組み合わせて、「クォート検出器(quote detector)」(チャネル985)と「クォートタイプ分類器(quote type classifier)」(チャネル460)という残差チャネルを生成します(Figure 4参照)。
- 文字列の終了: その後のレイヤー10のアテンションヘッド(10.attn.head82)が、「クォート検出器」をキー(Key)として、「クォートタイプ分類器」をバリュー(Value)として使用することで、対応するクォートを予測し、文字列を閉じます。
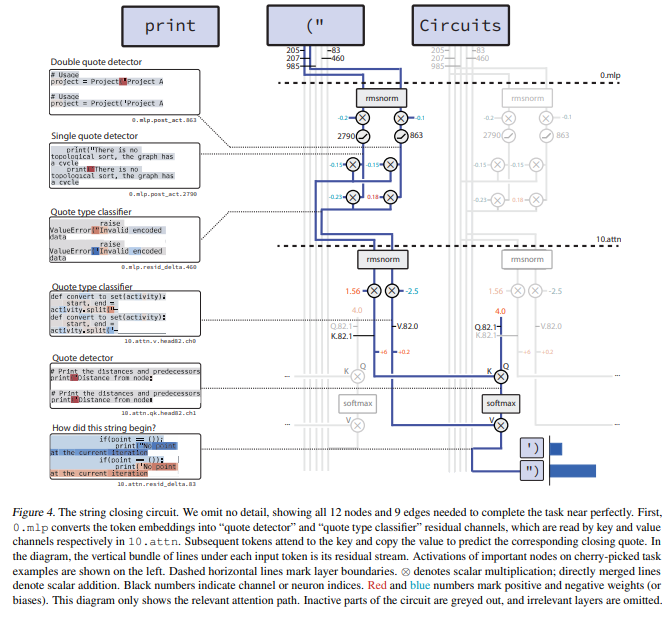
この回路を構成する4つのコンポーネントがネットワーク全体に持つ合計41のエッジのうち、この回路で使用されているのはわずか9つであり、この回路が非常に分離していることが示されています。
3.2.2. COUNTING NESTING DEPTH (ネストの深さのカウント)
リストのネストの深さに応じて ] または ]] でリストを適切に閉じるタスク(bracket counting)の回路が分析されました。このタスクの回路は以下の3ステップで機能します。
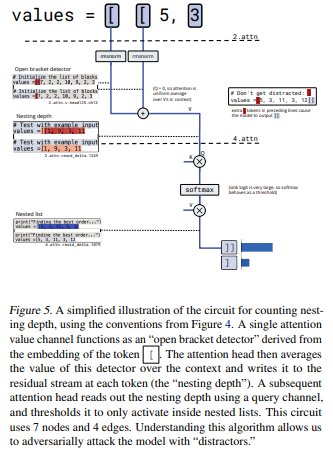
- 埋め込み(Embedding): トークン埋め込みの [ が残差チャネル(759, 826, 1711)に書き込まれ、これらが「ブラケット検出器」となります。
- カウント(Counting): モデルは、これらのブラケット検出器をレイヤー2の単一のバリューチャネル(ヘッド125、チャネル12)に集約し、これは「オープンブラケット検出器」として機能します。アテンションヘッド125は、コンテキスト全体でこの値の平均を計算し、残差チャネル1249に書き込みます。この残差チャネル1249のマグニチュードが「リストの深さ」を符号化します。(Figure 8参照)
- しきい値処理(Thresholding): リストの深さをバイナリ出力(]]を予測するかどうか)に変換するため、レイヤー4の別のアテンションヘッド(ヘッド80)が、リストの深さをクエリチャネルとして使用し、アテンションSoftmaxをしきい値として機能させます。これにより、ネストされたリスト内でのみ正の値を出力し、]]を出力します。
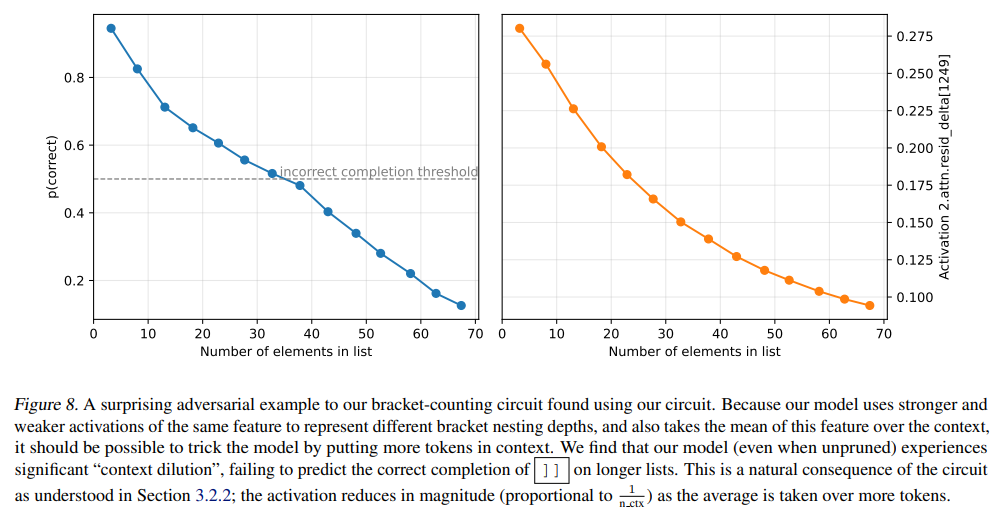
このメカニズム的な理解に基づき、コンテキスト内のトークン数を増やすとリストの深さを示す活性化のマグニチュードが「希釈」され、モデルが誤った予測をするという、自然な敵対的サンプル(Context Dilution)が発見されました。
3.2.3. TRACKING THE TYPE OF A VARIABLE (変数の型の追跡)
変数 current がセット(Set)型か文字列(String)型かを追跡し、その後の操作(.add または +=)を予測するタスクの回路が分析されました。これは2段階の「二段階ホップ(two-hop)」アルゴリズムを使用します。
- 情報コピー: レイヤー4のアテンションヘッド(ヘッド73)が、変数の初期化(例:current = set())時に、current の埋め込みを set() または “” トークンにコピーします。
- 情報取得: その後、モデルが current の値を呼び出す必要があるとき、レイヤー6のヘッド(ヘッド26)が current の埋め込みをクエリおよびキーとして使用し、最初のステップでコピーされた型情報(set() または “” の値)を最終トークン位置にコピーすることで、正しい操作を予測します(Figure 6参照)。

3.3. Using bridges to extract circuits from existing models (既存モデルから回路を抽出するためにブリッジを使用する)
本研究の主な成果は重みスパースモデルに基づいていますが、ブリッジを用いることで、訓練済みの密モデルの挙動理解にも応用できる可能性を示しました。
解釈可能な摂動(Interpretable Perturbations):ブリッジを使用することで、スパースモデルにおける「解釈可能な」活性化の摂動(関心のある特徴を変更する介入)を、対応する密モデルの活性化へとマッピングできます。
例えば、single double quote タスクにおいて、密モデルの「クォートタイプ分類器」チャネルを、ダブルクォートでプロンプトされたにもかかわらずシングルクォートの活性化に似るように操作したところ、密モデルがシングルクォートを出力する確率が急増しました(Figure 9参照)。これは、ブリッジを通じて、密モデルがクォートトークンに格納しているクォートタイプの表現を編集できたことを示唆しています。

4. Discussion (考察)
非効率性とスケーリングの限界:構造化されていない重みスパースなニューラルネットワークは、根本的な制約により、密なネットワークほどの効率を達成することは難しいです。したがって、この手法をフロンティアモデルの完全な解釈に直接適用したり、解釈可能なフロンティアモデルを一から訓練したりするのは困難です。
今後の方向性:
- モデル生物(Model Organisms)としての利用: スパースモデルをGPT-3程度の能力レベルまで拡張し、解釈可能な「モデル生物」として利用します。トランスフォーマーがスパースモデルと密モデルの両方で共通の回路モチーフを学習している可能性があり、これを研究することでフロンティアモデルの調査の指針を得ることができます。
- 狭いタスクへの応用: 計算資源を節約するため、欺瞞(deception)や拒否(refusal)といった、狭くも重要性の高いタスク分布に絞って、スパースブリッジモデルを訓練することが、AIの安全性確保(Safety Cases)のための貴重なツールとなる可能性があります。
- 自動解釈性との連携: スパース回路は、モデルの計算を理解するための新しいプリミティブ(基本要素)を提供し、自動化された解釈性研究をサポートします。
5. Limitations and Future Work (制約事項と今後の研究)
本研究の手法にはいくつかの制約があり、今後の改善の余地があります。
- 計算の非効率性: スパースモデルは、同等の能力を持つ密モデルと比較して、訓練と推論において大幅に(100〜1000倍)多くの計算資源を必要とします。これは、現代のGPUが疎行列演算に不向きな構造(Tensor Coresなど)を採用していることに起因します。
- 多義的な特徴 (Polysemantic features):より複雑なタスクの回路では、特徴が完全に単一の意味(monosemantic)を持つノードで構成されているわけではなく、一部の概念が複数のノードにわたって「塗られている(smeared)」(重ね合わせ)状態が残っています。
- 非バイナリ値の特徴: 抽出された特徴(活性化)の中には、オン/オフだけでなく、そのマグニチュード(大きさ)にも情報が含まれているものがあり、完全にバイナリ化(二値化)できません。
- 忠実性の定義: 回路がモデルの内部挙動を忠実に反映しているかの検証には平均アブレーション(Mean Ablation)が使用されていますが、これは完璧な測定方法ではありません。より厳密な検証には、因果的スクラビング(Causal Scrubbing)などの手法が必要です。
- スケーリングの不確実性: より複雑なタスクやより高性能なモデルを解釈しようとすると、回路が非常に大きく複雑になる可能性があり、本手法がどこまでスケールするかは不明確です。
まとめ
本稿でご紹介した研究は、トランスフォーマーモデルのメカニズム的解釈性において、重みスパース性という強力な誘導バイアスを導入することで、前例のないレベルの人間による理解可能性を達成しました。また、訓練済みの密なモデルの挙動を、重みスパースなモデルの表現に「ブリッジ」することで、解釈可能な摂動を密モデルに適用できる可能性を示し、既存のフロンティアモデルを解釈するための新しい道筋を切り開きました。
計算効率の課題は残りますが、本研究は、AIの内部理解を深め、将来的な安全性や信頼性を高める上で非常に重要な一歩といえます。今後の研究にも注視していきたいと思います。









