AIが解き明かす流体力学の謎：物理情報ニューラルネットワークによる「特異点」の新発見

はじめに

　本稿では、DeepMindの発表をもとにAI技術を用いて流体力学における長年の難問を解き明かす最新の研究成果について解説します。

　この研究は、物理法則を学習する特殊なAIを用いることで、流体の振る舞いを記述する複雑な方程式に潜む「特異点」と呼ばれる現象の、全く新しいファミリーを発見したものです。

参考記事

• タイトル： Discovering new solutions to century-old problems in fluid dynamics
• 著者： Yongji Wang, Sam Blackwell
• 発行日： 2025年9月18日
• URL：https://deepmind.google/discover/blog/discovering-new-solutions-to-century-old-problems-in-fluid-dynamics/

要点

• AI技術、特に物理情報ニューラルネットワーク（PINNs）を用いて、流体力学の基本方程式における新しい「特異点（ブローアップ）」のファミリーを発見した。
• このアプローチは、これまで発見が極めて困難だった「不安定な特異点」の体系的な発見を初めて可能にし、従来の手法では到達不可能な極めて高い精度を実現した。
• 発見された特異点には、不安定性の度合いとブローアップ速度の間に明確な数学的パターンが存在し、さらなる解の存在を示唆している。
• 本研究は、AIと数学的洞察を融合させ、コンピュータ支援による数学研究の新時代を切り開く可能性を示すものである。

詳細解説

流体力学と「特異点」とは？

　私たちの身の回りにある水や空気の流れ、すなわち「流体」の動きは、物理学の一分野である流体力学によって研究されています。ハリケーンの巨大な渦から、飛行機を空中に浮かせる翼周りの空気の流れまで、その応用範囲は非常に広範です。

　科学者たちは、これらの流体の動きを記述するために、何世紀にもわたって数学的な方程式を発展させてきました。しかし、これらの方程式には、理論上はあり得るものの、現実の物理世界では決して起こりえない特殊な状況、すなわち「特異点（singularity）」または「ブローアップ（blow up）」と呼ばれる解が存在します。これは、計算上、流体の速度や圧力といった物理量が無限大に発散してしまう点を指します。

　特異点の研究は、単なる理論上の遊びではありません。方程式がどのような条件下で破綻するのか、その限界を明らかにすることは、物理法則そのものへの理解を深める上で極めて重要です。特に、流体力学で最も有名かつ難解なナビエ–ストークス方程式における特異点の存在証明は、数学のミレニアム懸賞問題の一つにも挙げられています。

　特異点には、わずかな条件の変化にも耐えられる「安定なもの」と、極めて厳密な条件でのみ発生する「不安定なもの」があります。専門家は、ナビエ–ストークス方程式のような複雑な系では安定な特異点は存在しないと考えており、不安定な特異点の発見が、この分野の根本的な問いに答える鍵となると期待しています。

物理法則を学習するAI「PINNs」

　今回の研究の核心は、物理情報ニューラルネットワーク（Physics-Informed Neural Networks, PINNs）と呼ばれるAI技術の活用にあります。

　一般的なニューラルネットワークが、大量のデータセットからパターンを学習するのとは対照的に、PINNsは物理法則を記述する方程式そのものを学習します。AIが出力した解が、物理法則（方程式）とどれだけ食い違っているか（これを「残差」と呼びます）を常に計算し、その残差が最小になるように自らを訓練していきます。

　研究チームは、このPINNsに数学的な洞察を直接組み込むことで、従来の手法では捉えることが困難だった不安定な特異点のような解を発見する「発見ツール」へと昇華させました。さらに、その精度は驚異的なレベルに達しており、記事によれば「地球の直径を数センチの誤差で予測する」ことに匹敵するほどの正確さを実現したとされています。

新しい特異点ファミリーの発見とそのパターン

　この高精度な手法を用いて、研究チームは3つの異なる流体方程式（非圧縮性多孔質媒体（IPM）方程式、ブシネスク方程式など）において、これまで知られていなかった不安定な特異点の新しいファミリーを体系的に発見することに成功しました。

　さらに重要なのは、発見された特異点に驚くほど明確なパターンが見られたことです。下のグラフは、特異点の不安定さの度合い（横軸）と、ブローアップする速度を表すキーパラメータであるラムダ（λ）の値（縦軸）の関係を示しています。

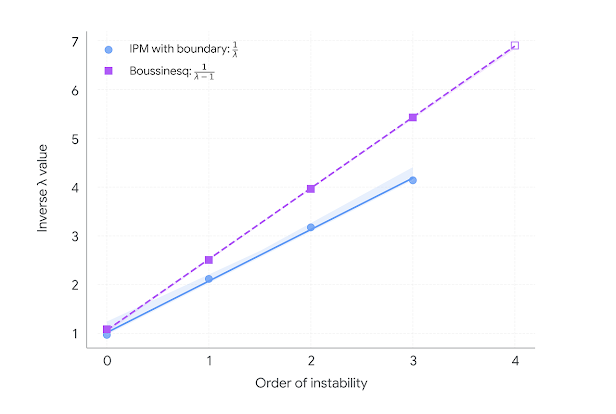
　この美しい線形関係は、非圧縮性多孔質媒体方程式とブシネスク方程式の両方で確認され、これらの特異点が偶然の産物ではなく、背後に共通の数学的構造が存在することを示唆しています。さらに、この直線上に位置するであろう、まだ見つかっていない、より不安定な解の存在を予測させます。

　研究チームはまた、発見した特異点の渦度（vorticity）場の可視化も行っており、これは流体の各点でどの程度回転しているかを示す重要な物理量です。これらの可視化により、特異点の物理的な構造をより深く理解できるようになりました。

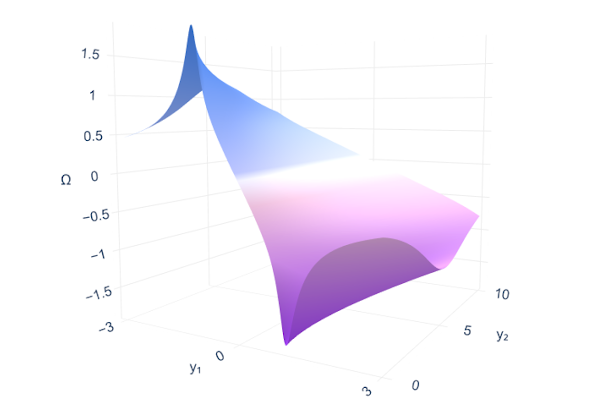
　上図のグラフは、研究した方程式の 1 つに対して見つかった 3 次元表現と 2 次元渦度 (Ω) フィールドの視覚化したものです。また、発見したすべての不安定性について、同じ場を軸に沿って一次元的に切断した図も示しており、特異点の不安定化が進行する様子を示しています。

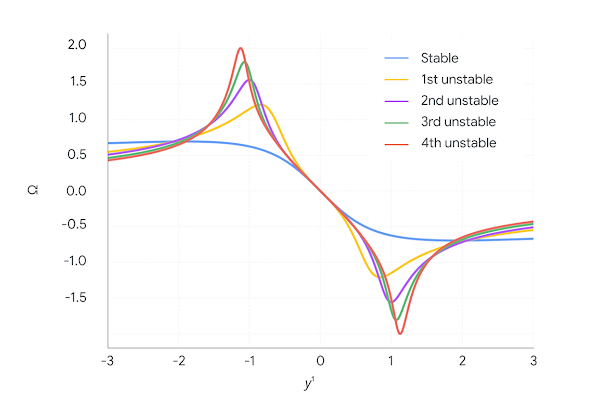
　上図の折れ線グラフは、上記と同じ二次元渦度（Ω）場の一次元的な切断図であり、特異点の不安定化が進行する様子を示しています。

コンピュータ支援数学の新時代 　

　この研究は、従来のPINNsの一般的な用途である偏微分方程式の数値解法を超えて、数学的発見のためのツールとしての新たな可能性を示しました。極めて高い精度を実現することで、厳密なコンピュータ支援証明に必要なレベルでの解析が可能となり、理論数学と計算数学の境界を曖昧にする成果となっています。

まとめ

　本稿で紹介した研究は、AIと人間の数学的洞察を組み合わせることで、流体力学という古典的な物理学の分野で、長らく未解決であった問題に新たな光を当てました。物理法則を学習するAI（PINNs）を用いることで、これまで捉えることのできなかった「不安定な特異点」を体系的に発見し、さらにその背後に潜む数学的なパターンまでも見出すことに成功しました。

　この成果は、単に流体力学の理解を深めるだけでなく、AIを駆使したコンピュータ支援による数学研究という、新しい研究スタイルの可能性を示すものです。今後、このアプローチが物理学や工学の他の分野にも応用され、さらなる科学的発見につながることが期待されます。