はじめに
近年、大規模言語モデル(LLM)をはじめとする深層学習モデルは目覚ましい進歩を遂げていますが、その能力向上は主に、より強力なニューラルアーキテクチャの開発と、それを効果的に訓練するための最適化アルゴリズムの設計に依存してきました。しかしながら、これらのモデルがどのように継続的に学習・記憶し、また、自ら改善しながら「効果的な解」を見つけるのかについて、根本的な課題と未回答の疑問が残されています。
特に、LLMは事前学習が完了すると静的な存在となりやすく、新しい知識を継続的に獲得することが困難です。その唯一の適応可能な要素は、入力されたコンテキスト内での迅速な適応を可能にする、文脈内学習(In-Context Learning)の能力に限定されます。この状態は、新しい長期記憶を形成できない「順行性健忘(anterograde amnesia)」という神経学的状態に類似していると指摘されています。
本稿では、この根本的な課題に取り組むため、深層学習アーキテクチャを再解釈する新しい学習パラダイム「Nested Learning (NL)」を提案する論文を紹介します。NLは、モデル全体を、それぞれが独自の「コンテキストフロー」を持つ、入れ子状(ネストされた)の最適化問題のセットとして一貫して表現します。これにより、既存の深層学習手法がどのように機能しているかを数学的に明確にし(ホワイトボックス化)、脳科学的な妥当性も持ちながら、より表現力の高い学習アルゴリズムを設計する道筋を提案しています。
解説論文
- 論文タイトル:Nested Learning: The Illusion of Deep Learning Architectures
- 論文URL:https://abehrouz.github.io/files/NL.pdf
- 発表学会:NeurIPS 2025
- 発表者:Ali Behrouz, Meisam Razaviyayn, Peiling Zhong, Vahab Mirrokni (Google Research, USA)
要点
Nested Learning (NL)の提唱により、従来の深層学習の課題を克服するための、以下の3つの主要な貢献がなされている。
- ディープ・オプティマイザ(Deep Optimizers)の提唱: 従来の勾配ベースの最適化手法(例:Adam、Momentum付きSGDなど)は、勾配を圧縮する連想記憶モジュールとして再解釈される。この視点から、より深い記憶や強力な学習ルールを備えた、表現力の高いオプティマイザの設計が可能になる。
- 自己修正型シーケンスモデルの実現: NLの洞察に基づき、自身の更新アルゴリズム自体を学習することで自己修正(Self-Modifying)する、新しいシーケンスモデル「Titans」の変種が提案された。
- 連続体記憶システム(Continuum Memory System)の定式化: 従来の「長期記憶/短期記憶」という概念を一般化し、異なる更新頻度を持つ多層的なフィードフォワードネットワークとして構成される新しい記憶システムが提案された。
これらを組み合わせた学習モジュールHOPEは、言語モデリング、継続学習、長期文脈推論タスクにおいて、既存のTransformerやモダンなリカレントニューラルネットワークを上回る有望な結果を示している。
詳細解説
論文の構成に従い、Nested Learning (NL) の詳細と、それが深層学習コンポーネントにもたらす新たな解釈について解説します。
1 Introduction(はじめに)
数十年にわたり、AI研究は勾配ベースの手法を用いてパラメータ \( \theta \in \Theta \) に対する目的関数 \( L(\theta) \) を最適化することで、データや経験から学習する機械学習アルゴリズムの設計に集中してきました。ディープラーニングの登場により、特徴抽出が自動化され、様々な分野で成功を収めました。
深層学習モデルにおける多層の積み重ねは、モデルの容量と表現力を高めます。しかし、この深い設計は万能ではなく、計算深さの限界、一部パラメータの容量の頭打ち、準最適な最適化、そして継続学習や汎化能力の不足といった課題が残されています。
これらの課題への対応として、より表現力の高いアーキテクチャの開発、より適切な目的関数の導入、効率的な最適化アルゴリズムの設計、そして適切な条件下でのモデルサイズのスケーリングといった努力が行われてきました。LLMの出現は、これらの進展の集大成です。
Current Models only Experience the Immediate Present(現在のモデルは直近の現在しか経験しない)
LLMは、コンテキスト内学習能力を持つものの、一般に初期の学習(事前学習)後は静的な状態にあり、継続的な新しい能力の獲得が困難です。
この静的な性質を、人間が新しい長期記憶を形成できない順行性健忘に例えています。現在のLLMの知識は、コンテキストウィンドウに入る「直近の文脈」か、または事前学習終了以前の「遠い過去」の知識を格納するMLP層に限られます。コンテキスト内で与えられた情報は、長期記憶パラメータ(フィードフォワード層)には影響を与えず、短期記憶(アテンション)に保持されている間しか有効ではありません。
1.1 Human Brain Perspective and Neurophysiological Motivation(人間の脳の視点と神経生理学的動機)
人間の脳の効率的な継続学習能力は、ニューロプラシシティ(神経可塑性)に起因すると考えられます。長期記憶の形成には、以下の二つの固定化プロセスが関与しています:
- 迅速な「オンライン」固定化(シナプス固定化): 学習直後や覚醒中に起こり、記憶痕跡を安定させ、短期から長期記憶への移行を始めます。
- 「オフライン」固定化(システム固定化): 海馬の活動と皮質の活動が協調して行われ、記憶を強化・再編成し、皮質部位へ転送します。
LLMの順行性健忘のアナロジーに戻ると、その静的な性質は、特にオンライン固定化フェーズが影響を受けていることに対応します。本稿の研究では、このオンラインでの記憶固定化プロセスに着目しています。

2 Nested Learning(ネストされた学習)
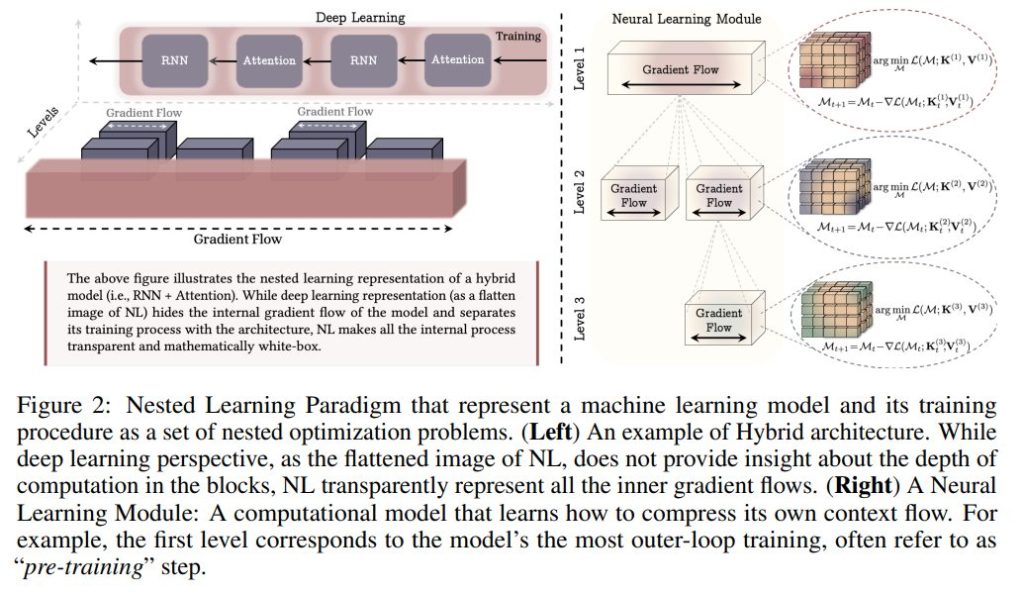
Nested Learning (NL) は、モデルを入れ子状の多レベルの最適化問題として表現する新しいパラダイムです。
2.1 Associative Memory(連想記憶)
連想記憶は、出来事間の関連を形成し、検索する基本的な精神プロセスであり、人間の学習に不可欠です。
本稿では、記憶を「入力によって引き起こされるニューラルな更新」と定義し、学習を「効果的で有用な記憶を獲得するプロセス」とします。NLでは、最適化手法やニューラルネットワークを含む計算シーケンスモデルのすべての要素が、自身のコンテキストフロー(データや勾配など)を圧縮する連想記憶システムであると見なされます。
連想記憶 ( M ) は、キーの集合 ( K ) と値の集合 ( V ) のマッピングを学習する演算子として定義されます:
$$ M^* = \underset{M}{\text{argmin}} \ \tilde{L}(M(K); V) \tag{1} $$
この定式化は、ネットワーク \( M(\cdot) \) がマッピングをパラメータに圧縮し、低次元空間で表現するための訓練プロセス(データ圧縮)としても解釈できます。
A Simple Example of MLP Training(MLP訓練の簡単な例)
1層MLPを勾配降下法で訓練するプロセスは、入力データ \( x_{t+1} \) を、目的関数が課す構造との不一致を示す「局所的驚き信号(Local Surprise Signal, LSS)」 \( u_{t+1} = \nabla_{y_{t+1}} L(W_t; x_{t+1}) \) にマッピングする、効果的な記憶(パラメータ \( W \)) を獲得するプロセスとして再定式化できます。この場合、モデルは単一の勾配フローを持ちます。(1層MLPの「単一の勾配フロー」とは、複雑なモデルに見られるような運動量項やアテンションメモリなど、異なる更新頻度を持つ階層的な「連想記憶」が存在せず、パラメータ W のみを更新するために一つの大きな誤差信号の流れが存在している、というシンプルな状況を表しています。)
次に、運動量付き勾配降下法(GD with Momentum)を考えると、運動量項 \( m_{t+1} \) は、過去の勾配をパラメータに圧縮するキーレス連想記憶として解釈できます。この分析により、運動量付き勾配降下法は、内側のレベル(運動量 \( m \) の最適化)と外側のレベル(重み \( W \) の更新)を持つ2レベルの最適化プロセスであることが明らかになります。
An Example of Architectural Decomposition(アーキテクチャ分解の例)
線形アテンション(Linear Attention)の記憶更新規則 \( M_t = M_{t-1} + v_t k_t^\top \) は、キーと値のマッピングを圧縮するための行列値連想記憶の最適化プロセス(勾配降下法)として再定式化されます。
このとき、線形アテンションの訓練プロセス(投影層 \( W_k, W_v, W_q \) の訓練)自体が、外側ループの連想記憶の最適化です。したがって、線形アテンションを勾配降下法で訓練する設定は、内側ループで記憶 \( M_t \) を最適化し、外側ループで投影層を最適化する2レベルの最適化プロセスとして見なされます。
さらに、線形アテンションを運動量付き勾配降下法で訓練する場合、線形アテンションの2レベル構造と、運動量付きGD自体の2レベル構造(運動量項が勾配を圧縮する記憶)が組み合わさり、より多階層の最適化プロセスとして表現されます。
2.2 Nested Optimization Problems(ネストされた最適化問題)
NLでは、脳波の階層性に着想を得て、各コンポーネントの更新頻度(Update Frequency, \( f_A \)) に基づいて、最適化問題を階層化します。更新頻度が高いほどレベルが低くなります(より内側のループ)。
更新頻度(Definition 2): コンポーネント \( A \) の頻度 \( f_A \) は、単位時間あたりの更新回数です。
コンポーネントの順序は、頻度、または頻度が等しい場合の計算依存性によって定義されます。この階層化に基づき、モデルの各コンポーネントは独自の勾配フローと最適化問題を保持します。
ニューラル学習モジュール(Neural Learning Module): NLは、機械学習モデルを、複数のレベルを持つコンポーネントが相互接続されたシステムとして表現する新しい方法です。深層学習が層の積み重ね(Flattened Image of NL)であるのに対し、NLは内部の勾配フローを透明化し、より多くのレベルを定義することで表現力を高めることが可能です。
2.3 Optimizers as Learning Modules(学習モジュールとしての最適化手法)
NLの視点では、勾配ベースのオプティマイザは、モデルの勾配をそのパラメータに圧縮するメタ記憶モジュールとして機能します。
Extension: More Expressive Association(拡張:より表現力の高い連想)
運動量項は「値を持たない連想記憶」であり、表現力が限られています。これを改善するため、値パラメータ \( P_i \) を導入し、運動量項が \( P_i \) と勾配項 \( \nabla L(W_i; x_i) \) のマッピングを圧縮するように学習させます。これはプリコンディショニング(Preconditioning)付きGDと等価であり、運動量記憶が勾配を対応する値にマッピングする連想記憶として機能することを明確にします。
Extension: More Expressive Objectives(拡張:より表現力の高い目的関数)
運動量項の内部目的関数として、ドット積類似性の代わりに \( \ell_2 \) 回帰損失 \( | m \nabla L(W_i; x_i)^\top – P_i |^2_2 \) を使用すると、更新規則はデルタルールに基づいたものとなり、記憶(運動量)の限られた容量をより良く管理し、過去の勾配の系列をより効果的に記憶することができます。
Extension: More Expressive Memory(拡張:より表現力の高い記憶)
運動量が線形層(行列値)であることによる表現力の限界を克服するため、運動量記憶モジュールとしてMLPを用いることができます。これにより、勾配の基礎にある非線形なダイナミクスを捉えるための容量が増加し、Deep Momentum Gradient Descent (DMGD) として定式化されます。
Extension: None Linear Outputs(拡張:非線形出力)
運動量記憶モジュールの出力に非線形性 \( \sigma(\cdot) \) を適用することで、表現力をさらに強化できます。例えば、\( \sigma(\cdot) \) にニュートン・シュルツ法を適用し、線形層の \( m(\cdot) \) を使用すると、これはMuonオプティマイザと等価になります。
Going Beyond Simple Backpropagation(単純な誤差逆伝播を超える)
事前学習プロセスも連想記憶の一種ですが、従来の定式化はデータサンプル間の依存関係を無視する可能性があります。
データポイントの依存関係を考慮するため、\( L_2 \) 回帰目的関数を用いた以下の定式化が提案されます:
$$ \min_W \ | W x_t – \nabla_{y_t} L(W_t; x_t) |^2_2 \tag{27} $$
これにより、新しい勾配降下法の変種が導かれ、これはHOPEアーキテクチャの内部オプティマイザとして利用されます。
3 HOPE: A Self-Referential Learning Module with Continuum Memory(HOPE:連続体記憶を備えた自己参照型学習モジュール)
従来のLLMは、アテンション(ワーキングメモリ)とFFN(持続的知識貯蔵庫)で構成されますが、継続学習におけるLLMの静的な性質を克服するため、NLの知見に基づき、従来の記憶システムの視点が拡張されます。
連続体記憶システム(Continuum Memory System, CMS): CMSは、複数のMLPブロック \( \text{MLP}^{(f_1)}(\cdot), \dots, \text{MLP}^{(f_k)}(\cdot) \) をチェーン状に結合したもので、各ブロックは異なる更新頻度 \( f_\ell \) に対応するチャックサイズ \( C^{(\ell)} \) で更新されます。 パラメータ \( \theta^{(f_\ell)}t \) は、以下の規則に従って \( C^{(\ell)} \) ステップごとに更新されます:
$$ \theta^{(f\ell)}{i+1} = \theta^{(f\ell)}i – \begin{cases} \sum{t=i-C^{(\ell)}}^{i} \eta^{(\ell)}t f(\theta^{(f\ell)}_t; x_t) & \text{if } i \equiv 0 \pmod{C^{(\ell)}}, \ 0 & \text{otherwise}. \end{cases} \tag{31} $$
これは、各パラメータが自身のコンテキストを圧縮し、抽象的な知識を代表していることを意味します。
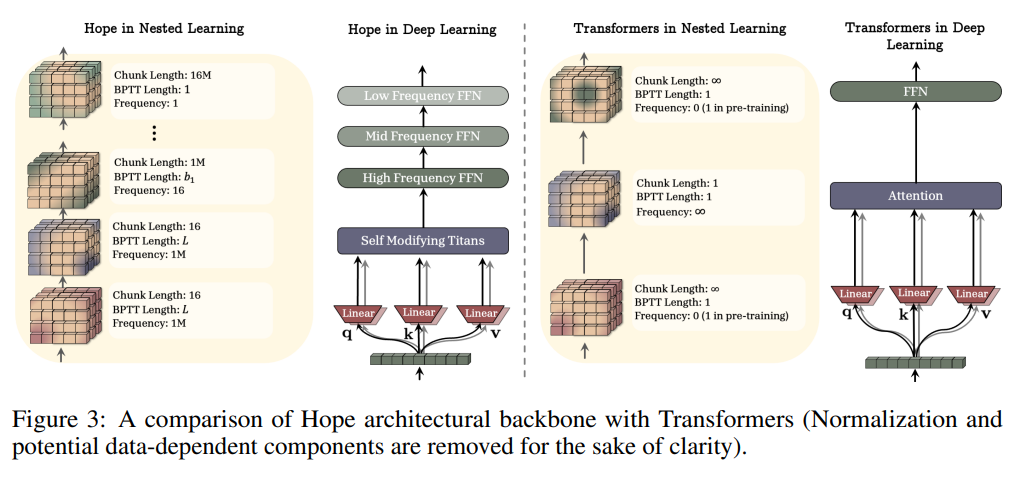
HOPE: このCMSと、自己参照型学習モジュール(Section 2.3で導入された勾配降下法の変種を使用)を組み合わせた新しいアーキテクチャがHOPEです。HOPEは、低周波数から高周波数まで複数のFFN層を持ち、Transformer(Figure 3を参照)とは異なり、多階層的な更新頻度を導入しています。
4 Experiments(実験)
HOPEは、言語モデリングおよび常識推論タスクにおいて、760Mおよび1.3Bパラメータのモデルサイズで評価されています。(Table 1参照)
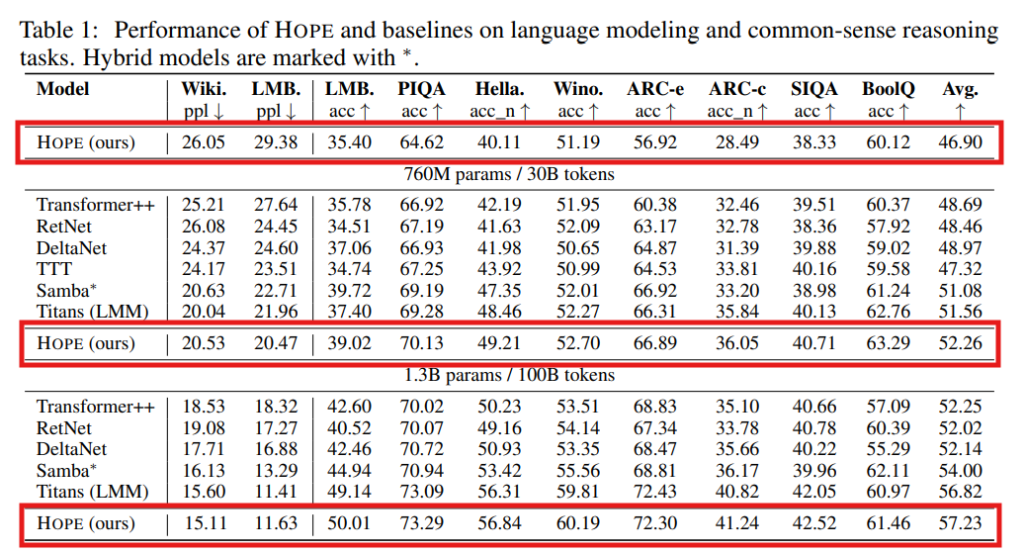
HOPEは、TransformerやRetNet、DeltaNet、Titansといったモダンなリカレントニューラルネットワークを含むベースラインと比較して、一貫して非常に良好なパフォーマンスを示しています。特に、HOPEは、コンテキストに基づいてキー、値、クエリの投影を動的に変更する機能と、深い記憶モジュール(CMS)を組み合わせることで、低いパープレキシティ(言語モデリングの評価指標、低いほど高性能)と高い精度(常識推論タスク)を実現しています。例えば、1.3Bパラメータのモデルでは、HOPEは最高の平均スコア(57.23)を達成しています。
まとめ
本稿では、深層学習モデルの設計と最適化に新たな次元をもたらすNested Learning (NL)のパラダイムと、それに基づく革新的なHOPEアーキテクチャについて解説しました。
NLは、すべての深層学習コンポーネントを、異なる時間スケールと頻度で更新される連想記憶としての最適化問題の階層として捉え直すことで、深層学習の内部メカニズムを数学的に透明化しました。この知見は、従来の最適化手法を拡張したディープオプティマイザの設計を可能にし、さらには脳の記憶固定化メカニズムに着想を得た連続体記憶システム(CMS)へと繋がりました。
CMSと自己参照型学習モジュールを統合したHOPEは、従来のLLMが抱える継続学習の課題を克服し、マルチタイムスケールで情報を処理する能力を示しています。これは、今後のAIモデルが、より人間らしい効率と適応性を持って、継続的に学習し、新しい知識を獲得していくための重要な基盤となるでしょう。









